Manacher

Manacher（马拉车）能在 O(n) 的时间复杂度内求出字符串中以字符i为中心的最长回文半径r[i]

算法流程

预处理

为了避免奇偶性问题

在字符串开始加上奇怪的 @

在字符串末尾加上&

在字符中间加上 #

本段代码来自可爱的w++ 并且把他老婆inline删掉了

void Init() {
    scanf("%s", s1 + 1);
    int len = strlen(s1 + 1);

    //构建新串
    n = 0;
    s[++n] = '#';
    for (int i = 1; i <= len; i++) {
        s[++n] = s1[i];
        s[++n] = '#';
    }
    s[0] = '@';
    s[n + 1] = '&';
}

---

求r数组

两个辅助变量mx，p

mx表示当前覆盖到的最右边界

p表示当前的中心位置

显然mx=p+r[p]

计算时 我们先求出r[i]的下界（最小值）

然后 直接向左右暴力扩展

令j为i关于p的对称点 j=p*2-i（中点坐标公式）

求i的下界时 有三种情况

1. mx<=i （完全不覆盖） r[i]=1

2. mx-i>r[j] （完全覆盖）r[i]=r[j] 因为i和j是对称的

3. mx-i<=r[j] (部分覆盖) r[i]>=mx-i

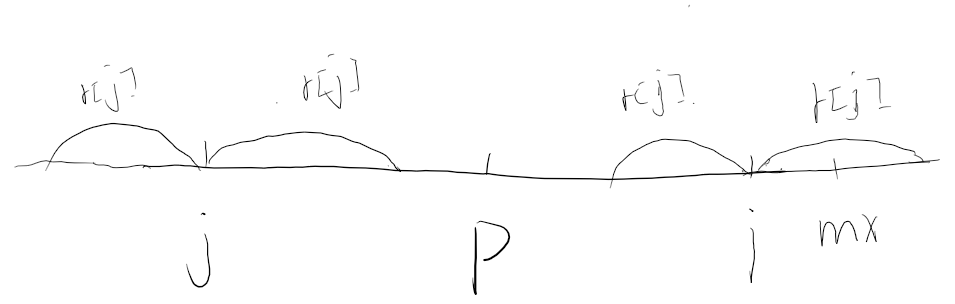
算完r[i]的下界后暴力向左右扩展即可

---

时间复杂度

因为mx必只向右移动n次

枚举i也是n次

所以总复杂度为O(n)级别

代码

void manacher()
{
    int p=0,mx=0;
    for(int i=1;i<=n;i++)
    {
        if(i<mx) r[i]=min(mx-i,r[p*2-i]);//第2 3种情况合并一下
        else r[i]=1;//第1种情况
        while(s[i-r[i]]==s[i+r[i]]) ++r[i];//向左右扩展
        if(i+r[i]>mx)
        {
            mx=r[i]+i;
            p=i;
        }
    }
}

题目

P4555 [国家集训队] 最长双回文串

//维护最长回文半径的同时,
//再分别维护两个东西，
//以i为结尾的最长回文子串的长度l[i]
//和以i为开头的最长回文子串的长度r[i]
//因为每个双回文串中间不能交叉
//即i只能是‘#’
//所以只能枚举i=='#'来找答案
#include<bits/stdc++.h>
using namespace std;
#define ll long long
const int N=1e5+100;
int n,len[(N<<1)+10],l[(N<<1)+10],r[(N<<1)+10];
char ch[N+10],s[(N<<1)+10]; //原数组 改后数组
void manacher()
{
    int p=0,mx=0;
    for(int i=1;i<=n;i++)
    {
        if(i<mx) len[i]=min(mx-i,len[p*2-i]);//第2 3种情况合并一下
        else len[i]=1;//第1种情况
        while(s[i-len[i]]==s[i+len[i]]) ++len[i];//向左右扩展
        if(i+len[i]>mx)
        {
            mx=len[i]+i;
            p=i;
        }
        l[i+len[i]-1]=max(l[i+len[i]-1],len[i]-1);//回文串真实长度为len[i]-1
		r[i-len[i]+1]=max(r[i-len[i]+1],len[i]-1);
		//这里只处理了以i为中心的最长回文串 所以之后要再处理l r数组
    }
}

int main()
{
    scanf("%s",ch+1);
    int tlen=strlen(ch+1);
    s[0]='$';
    s[1]='#';
    n=1;
    for(int i=1;i<=tlen;++i)
	{
		s[++n]=ch[i];
		s[++n]='#';
	}
	manacher();
	for(int i=3;i<=n;i+=2)r[i]=max(r[i],r[i-2]-2);
	//+=2是因为枚举的是# 中间差2 每差一个# 原串的长度也少2（左右各一个）所以-2
	for(int i=n;i>=3;i-=2)l[i]=max(l[i],l[i+2]-2);
	int ans=0;
	for(int i=3;i<=n;i+=2)if(r[i]&&l[i])ans=max(ans,l[i]+r[i]);//要写r[i]&&l[i]
	printf("%d\n",ans);
    return 0;
}

字符串连接—YbtOJ

manacher求回文串，后得到线段，做一点计算映射回原串线段。

然后问题转化为可重叠区间线段覆盖问题，可以贪心解决。

排序左端点，同一左端点取最长段，然后在此段中找到右端点最靠右的线段，线性更新并累加。

#include<bits/stdc++.h>
using namespace std;
const int maxn=200010;
int n,p[maxn];
char s[maxn],ss[maxn];
struct cyc
{
    int l,r;
} a[maxn];
bool cmp(cyc a,cyc b)
{
    return a.l<b.l||(a.l==b.l&&a.r>b.r);
}
void manacher()
{
    memset(p,0,4*(n+1));
    int id=0,mx=0;
    for(int i=1; i<=n; i++)
    {
        if(mx>i)
            p[i]=min(p[id*2-1],mx-i+1);
        else p[i]=1;
        while(s[i+p[i]]==s[i-p[i]]) p[i]++;
        if(i+p[i]-1>mx)
        {
            mx=i+p[i]-1;
            id=i;
        }
        if(i%2) a[i].l=i/2-p[i]/2+1,a[i].r=i/2+p[i]/2;
        else a[i].l=i/2-p[i]/2+1,a[i].r=i/2+p[i]/2-1;
        if(a[i].l>a[i].r)
            a[i].l=a[i].r=1;
    }
}
int main()
{
    while(scanf("%s",ss+1)==1)
    {
        int tot=strlen(ss+1);
        n=1;
        s[0]='$';
        s[1]='#';
        for(int i=1; i<=tot; i++)s[++n]=ss[i],s[++n]='#';
        manacher();
        sort(a+1,a+n+1,cmp);
        int right=a[1].r,ans=1,mx=0;
        for(int i=2; i<=n; i++)
            if(a[i].l!=a[i-1].l)
            {
                if(a[i].l>right+1)ans++,right=mx;
                mx=max(mx,a[i].r);
            }
        if(right<tot)ans++;
        printf("%d\n",ans-1);
    }
    return 0;
}