左偏树

Copyright By @

前言

左偏树是一棵向左偏的树

---

左偏树是一种能在$O(\log n)$之内完成合并的可并堆

长这样

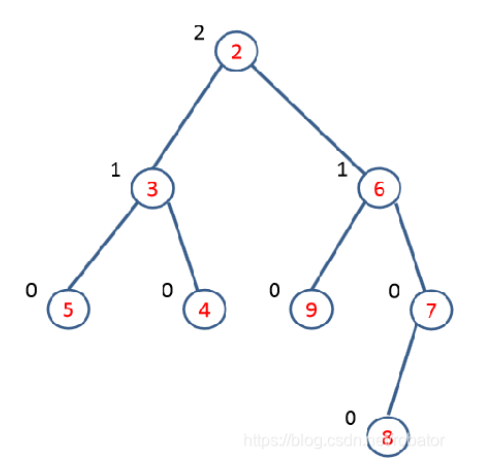
我们常用左偏树完成以下操作

1. 在指定集合中插入一个元素
2. 查询集合中最高优先级的元素
3. 删除集合中最高优先级的元素
4. 删除指定元素
5. 合并两个集合

---

性质

首先 我们要知道左偏树的每个节点都维护了什么东西

1. 左右子节点 父亲节点 （父亲孩子表示法）
2. 键值key （上文提到的优先级）其实就是我们要维护的数据（@某人说所有东西都是数据）

补一个定义

左子树或右子树为空的节点称为外节点，左子树和右子树可以同时为空。

3. 距离dist 不是外节点的节点 的距离为其到子树中最近的外节点的距离，外节点 的距离为0，空节点 的距离为-1

---

然后我们就可以说左偏树的一些性质了

1.节点的键值小于等于左右子节点的键值

说白了就是 键值满足小顶堆的性质

这个性质保证了我们可以在O(1)的时间复杂度内查询最小值(就是堆顶呀)

2.结点的左子结点的距离不小于右子结点的距离

这就是左偏树为什么叫左偏树的原因

3.节点的距离等于它的右子节点的距离加1

注意距离的概念跟深度不同 左偏树并不一定是左边节点数或深度大于右边的树

---

操作

合并

把两棵左偏树A，B合并成一棵左偏树C

1.最简单的情况就是一棵树为空 直接返回另一棵树即可

if(!A) return B;
if(!B) return A;

2.若不为空 假设A的根节点的键值小于B的根节点的键值（大于的话换一下不就好啦）那么把A的根节点作为C的根节点，递归合并A的右子树和B

if(key[B]<key[A]) swap(A,B); //B小于A的话就换一下
r[A]=Merge(r[A],B); //递归合并

3.合并之后 r[A]的距离可能变大 性质2可能被破坏 如果破坏了 需要交换一下A的左右子树

if(dist[r[A]]>dist[l[A]]) swap(l[A],r[A]); //不满足左偏性质 交换左右子树

4.r[A]的距离可能被改变，要更新A的距离

if(!r[A]) dist[A]=0;
else dist[A]=dist[r[A]]+1; //更新距离
return A; //合并好了 返回一下

合并的总代码为

int Merge(int A,int B)
{
    if(!A) return B;
    if(!B) return A;
    if(key[B]<key[A]) swap(A,B); //B小于A的话就换一下
    r[A]=Merge(r[A],B); //递归合并
    if(dist[r[A]]>dist[l[A]]) swap(l[A],r[A]); //不满足左偏性质 交换左右子树
    if(!r[A]) dist[A]=0;
    else dist[A]=dist[r[A]]+1; //更新距离
    return A; //合并好了 返回一下
}

---

单点插入

单个结点也可以看成一棵左偏树

所以可以看作合并操作

void Insert(int x,int A) //把x插入到A中
{
    int B=MakeIntoTree(x); //新建一棵只有根节点的左偏树
    A=Merge(A,B); //合并
}

---

删除根结点

将根结点的左右子树合并即可

int DeleteMin()
{
    int t=key[root];
    root=Marge(l[root],r[root]);//合并左右子树
    return t;
}

---

构建一棵左偏树

法1：将结点一个个单点插入（谁(sei)还那么做啊~）

梅姐附体

时间复杂度$O(n\log n)$

法2：

1.将结点放入到队列中

2.从队首取出两棵树 合并后插入队尾

3.当队列中只剩下一棵树时结束

时间复杂度$O(n)$

代码长介样

void Build()
{
    //此处节点队列为h，头尾为l、r
    int l=1,r=n;
    for(int i=1;i<n;i++)//可证只有n-1次合并
    {
        int root=Merge(h[l],h[l+1]);
        r++;
        h[r]=root;
        l+=2;
    }
}

---

删除任意已知结点

左偏树不能有效搜索指定键值的结点。

因为它只是堆 不是二叉搜索树

所以删除任意已知节点，首先要找到这个已知节点

需要遍历一遍，在O(n)的时间里找到这个节点。

找到这个结点后，设要删除的节点为x，合并x的左右子树，然后自底向上维护距离值，不满足左偏性质则交换左右儿子，直至距离值无需更新时，算法结束。

具体而言，设q是x的父节点。合并左右儿子后的新树设为p，即p=Merge(left(x),right(x))，设节点x的父节点为q，具体分析如下：

（1）x是原树中的根节点，则删除x节点后，合并左右子树后，算法结束

（2）x不是原树中的根节点，合并后的树为p，新的距离为dist(p),dist(p)与dist(q)的值相比有如下几种情况

（a） dist(p)=dist(q)-1 满足左偏条件，不需进行交换

（b）dist(p)<dist(q)-1

如果p是q的右子树，则需要更新q的距离值，并一直更新到距离值无需再更新时为止

如果p是q的左子树，则需要交换p和right(q)，并更新q的距离值，并一直更新到距离值无需再更新时为止

期间不满足左偏条件的要进行交换

（c）dist(p)>dist(q)-1

如果新树p在q的左子树上，则满足左偏条件，不需要交换和更新。

如果新树p在q的右子树上，如果新树p的距离大于q的左子树的距离，则需要交换，同时更新其q的距离，并一直更新到距离值无需再更新时为止，期间不满足左偏条件的要进行交换。

void Delete(int x)
{
    int q=parent[x];
    int p=Marge(l[x],r[x]);
    parent[p]=q;
    if(q && l[q]==x) l[q]=p;
    if(q && r[q]==x) r[q]=p;
    while(q)
    {
        if(dist[l[q]]<dist[r[q]])
            swap(l[q],r[q]);
        if(dist[r[q]]+1==dist[q]) return ;
        dist[q]=dist[r[q]]+1;
        p=q;
        q=parent[p];
    }
}

---

左偏树的基本操作就完事啦

关键还是合并操作

完结撒花

---

附上一道模板题

P3377【模板】左偏树/可并堆 - 洛谷

再附上两道题

P1552 [APIO2012] 派遣 - 洛谷

P3261 [JLOI2015] 城池攻占 - 洛谷

---

引用来源

左偏树简介-CSDN博客

还有书

---

每日一推

人生马拉松 - 陈奕迅

想起了元旦的小品

学习不是马拉松，而是百米赛跑

学习不是百米赛跑，而是马拉松