K-D树

前言

kd-tree（k-dimensional树的简称），是一种对k维空间中的实例点进行存储以便对其进行快速检索的树形数据结构。主要应用于多维空间关键数据的搜索（如：范围搜索和最近邻搜索）

~~好像跟没说一样~~

K-D树其实是每个结点为K维数值点的二叉树

每个结点将某一维划分成两部分

一部分为左子树

一部分为右子树

所以说，当 $k=1$ 时，kd树每个点都只划分这一维，其实是二叉搜索树

在我们算法竞赛中，通常 $k=2$

下面这棵树就是 $k=2$ 的

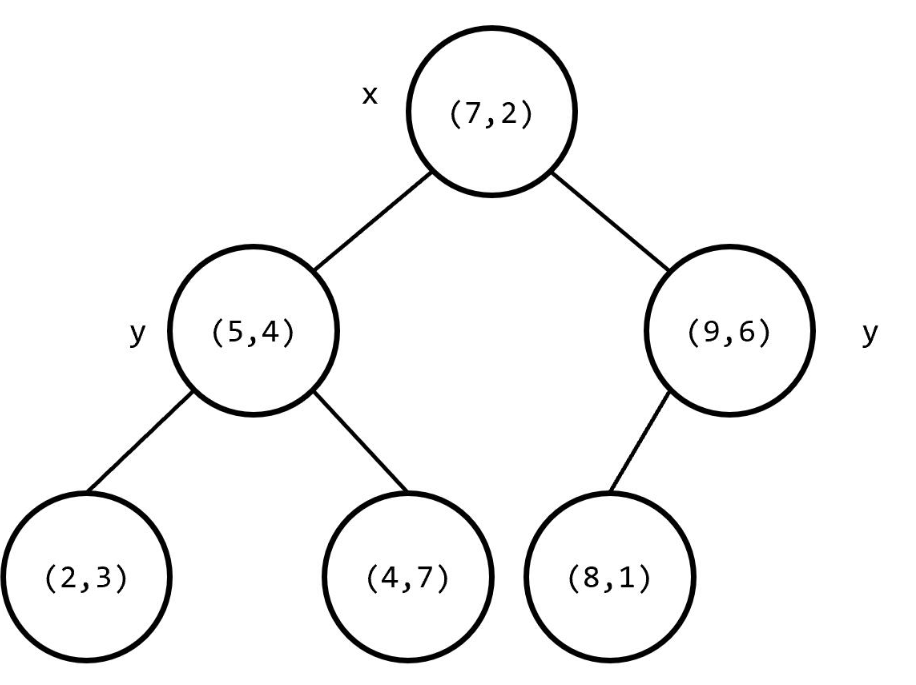
它的结点交替地分了一维和二维就像这样

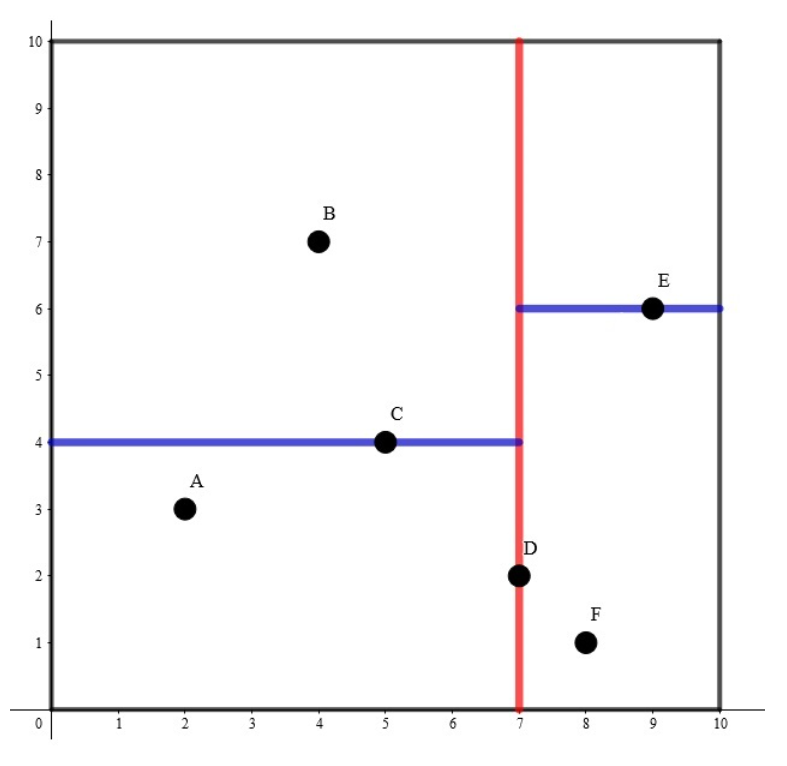
红线是按照根结点 $(7,2)$ 的x维分的

蓝线是结点 $(7,2)$ 的左右子结点 $(5,4)$ $(9,6)$ 的y维分的

下次再按子节点的x维分

......

这就是K-D树的一种建树方法：每一维交替建树

那么我们就开始说如何建树

操作

建树

K-D树建树的一般过程为：

选择某个维度
取数据在该维度的中位数（可以使左右子树的大小相等）作为分割的线
将小于中位数的数据点放到左子树
将大于等于中位数的数据点放到右子树

这就引出了两个问题

如何选择维度
如何计算中位数

划分维度的选择

有三种方法

k维交替建树(离线)

就是按顺序每一维依次划分

上面的例子就是这种方法按照x和y依次划分的

操作的时候可以用取余运算

第 $i$ 层按照 $i$ $mod$ $k$ 维划分

最大方差法(离线)

第一种方法并不是最优的

对于一组数据方差越大数据越分散（~~初中数学~~）

所以从方差大的维度分 可以更优

不过谁(sei)还这么做啊

~~梅姐又附体~~

3.动态插入法(在线)

把每一个点依次插入不平衡就拍扁重建插入操作在后面

为了方便，在算法竞赛中，最常用的是第一种方法

计算中位数

有个stl就可以计算(狂喜)

nth_element(ps+1,ps+mid,ps+r,cmp);

表示对 $ps$ 数组中下表为 $[l,r)$ 的元素按cmp的规则重新布置(没排序)，使得 $ps[mid]$ 存放着中位数，小于等于中位数的放在 $[l,mid]$ 中(没排序)，大于中位数的放在 $[mid+1,r]$ 中(没排序)

之后我们就可以建树了

代码长介样

~~跟线段树好像~~

int build(int l,int r,int wd)
{
    if(l>r)return 0;
    int mid=(l+r)>>1,k=newnode();
    WD=wd;//每次按照当前维度排序
    nth_element(p+l,p+mid,p+r+1,cmp);
    t[k].pt=p[mid];
    t[k].lc=build(l,mid-1,wd^1);
    t[k].rc=build(mid+1,r,wd^1);
    update(k);
    return k;
}

插入

类似于BST的插入

到每一维判断该是左右哪个子树就好

void ins(int &k,point tmp,int wd)
{
    if(!k)//新建节点
    {
        k=newnode();
        t[k].lc=t[k].rc=0;
        t[k].pt=tmp;
        update(k);
        return ;
    }
    if(tmp.x[wd]<=t[k].pt.x[wd])ins(t[k].lc,tmp,wd^1);
    else ins(t[k].rc,tmp,wd^1); 	//判断应该插入进左子树还是右子树中
    update(k);
}

但是插入多了就会不平衡

所以可以像替罪羊树一样设一个平衡因子

对于~~看不惯的~~不平衡的直接拍扁重建

@ 某人的逆天发言