- zyssssss 的博客
网络流&&费用流
- @ 2024-1-16 7:55:56
网络流
前言
当听到网络 流量之后 感觉是在充话费
网络流(network-flows)是一种类比水流的解决问题方法,与线性规划密切相关。
它模拟了水流从起点经过复杂的网络流向终点的过程
就像自来水厂的水 经过无数根水管子 流到了家里
而最大流就是最多有多少水流到了家里
算法流程
EK算法
首先,引入增广路的概念。
一条从s到t的路径,水流流过这条路,使得当前可以到达t的流量可以增加。
知道了增广路的概念,就可以很显然的想出一种贪心做法,不断通过bfs寻找增广路并处理和累加答案,直到找不到增广路,答案就是最大流。
但是它是错的
如图
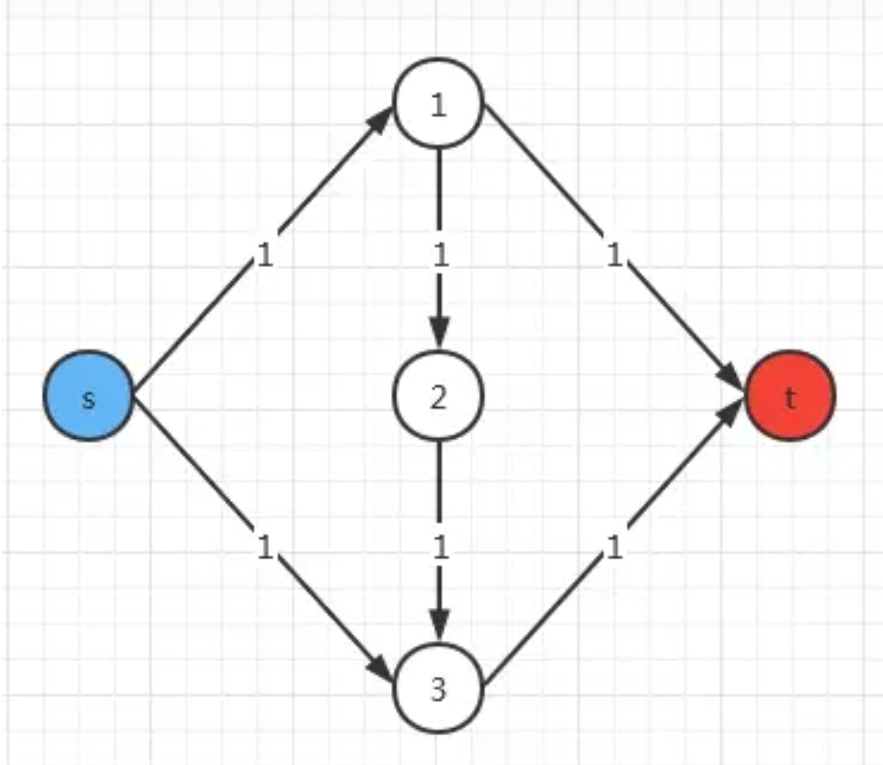
如果我们找到了s-1-2-3-t 这条路径 流量为1
那么图会变成这样
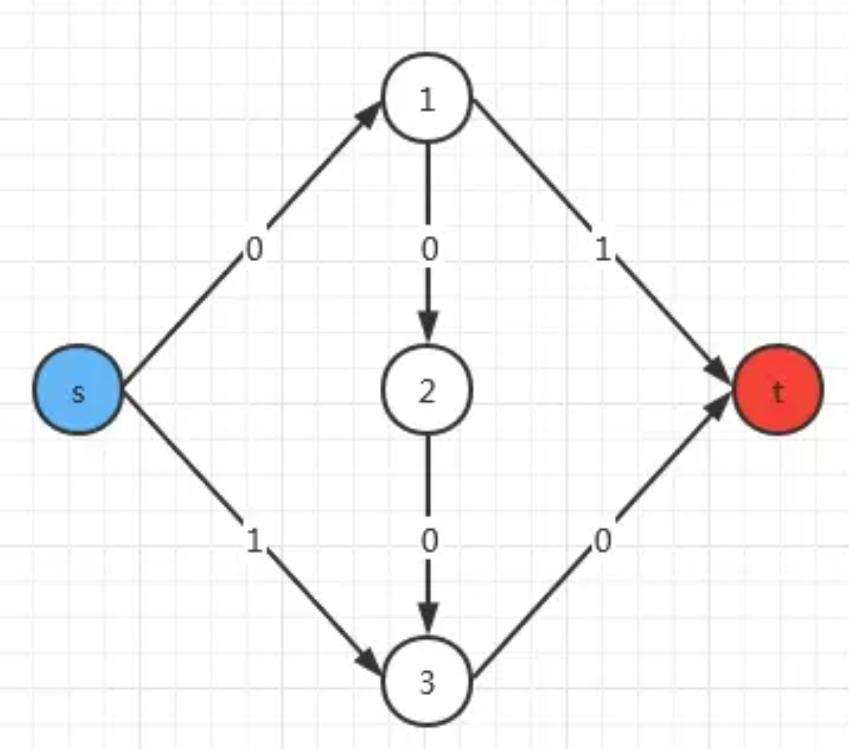
再找不到了增广路了 但是显而易见原图的最大流是2
所以 我们引入了后悔药反向边
在流量减去最小值的时候,将反向边加上最小值
就像这样
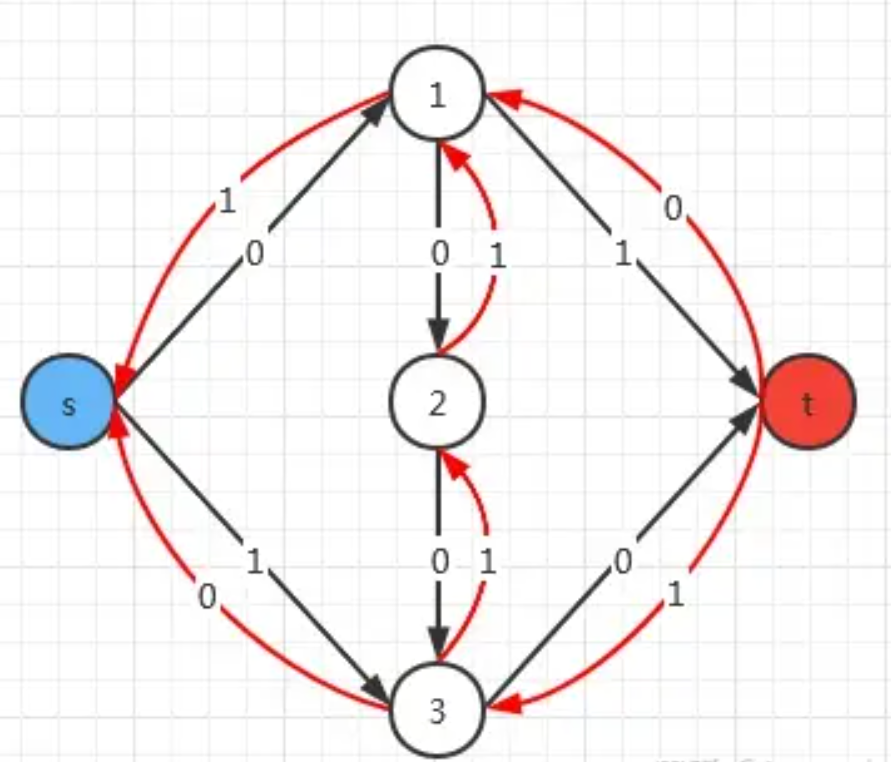
于是多了一条增广路 s-3-2-1-t
综上所述 我们得到了一种求最大流的方法
总结一下就是
通过没流满的边或新建的反向边找增广路增广
在找不到增广路时算法结束
其实这个思想就是EK算法的思想
代码大概是这样的
#define maxn 250
#define INF 0x3f3f3f3f
struct Edge {
int from, to, cap, flow;
Edge(int u, int v, int c, int f) : from(u), to(v), cap(c), flow(f) {}
};
struct EK {
int n, m; // n:点数,m:边数
vector<Edge> edges; // edges:所有边的集合
vector<int> G[maxn]; // G:点 x -> x 的所有边在 edges 中的下标
int a[maxn], p[maxn]; // a:点 x -> BFS 过程中最近接近点 x 的边给它的最大流
// p:点 x -> BFS 过程中最近接近点 x 的边
void init(int n) {
for (int i = 0; i < n; i++) G[i].clear();
edges.clear();
}
void AddEdge(int from, int to, int cap) {
edges.push_back(Edge(from, to, cap, 0));
edges.push_back(Edge(to, from, 0, 0));
m = edges.size();
G[from].push_back(m - 2);
G[to].push_back(m - 1);
}
int Maxflow(int s, int t) {
int flow = 0;
for (;;) {
memset(a, 0, sizeof(a));
queue<int> Q;
Q.push(s);
a[s] = INF;
while (!Q.empty()) {
int x = Q.front();
Q.pop();
for (int i = 0; i < G[x].size(); i++) { // 遍历以 x 作为起点的边
Edge& e = edges[G[x][i]];
if (!a[e.to] && e.cap > e.flow) {
p[e.to] = G[x][i]; // G[x][i] 是最近接近点 e.to 的边
a[e.to] =
min(a[x], e.cap - e.flow); // 最近接近点 e.to 的边赋给它的流
Q.push(e.to);
}
}
if (a[t]) break; // 如果汇点接受到了流,就退出 BFS
}
if (!a[t])
break; // 如果汇点没有接受到流,说明源点和汇点不在同一个连通分量上
for (int u = t; u != s;
u = edges[p[u]].from) { // 通过 u 追寻 BFS 过程中 s -> t 的路径
edges[p[u]].flow += a[t]; // 增加路径上边的 flow 值
edges[p[u] ^ 1].flow -= a[t]; // 减小反向路径的 flow 值
}
flow += a[t];
}
return flow;
}
};
概念&&性质
我们需要补充几个概念
不学好像也行?
- 在网络流中,有一个源点s,还有一个汇点t,边的权值称为容量,且边为有向边
- 边的当前的流量应该小于等于容量(不然水管不就爆了)
- 边的当前的流量等于反向边的流量的相反数
- 每个中间点流入的等于流出的
- 整个图的流量为从源点出发的流量之和(流入汇点的之和)
- 残量网络:没流满的边和反向边所形成的图(找增广路其实就是在它上面找的)
所以EK算法就是在残量网络上求增广路的算法
还有对它正确性的证明 利用了最大流等于最小割
Dinic算法
Dinic算法是EK算法的优化
它有三处优化
- 分层图优化:在增广之前跑BFS建出分层的残量网络,可以同时多路增广
- 当前弧优化:将链式前向星的第一条边传址调用 直接修改它的值
- -1优化:在同一次DFS中 一个点无法引出任意增广路 直接删掉
好像多路增广不算优化 OI Wiki上这么说的
可能是由于大量网络资料的错误表述引发以讹传讹的情形,相当数量的选手喜欢将当前弧优化和多路增广并列称为 Dinic 算法的两种优化。实际上,当前弧优化是用于保证 Dinic 时间复杂度正确性的一部分,而多路增广只是一个不影响复杂度的常数优化。
利用这三个优化 EK算法就成了Dinic算法
struct MF
{
struct edge
{
int v, nxt, cap, flow;
} e[N];
int head[N], cnt = 0;
int n, S, T;
ll maxflow = 0;
int dep[N], cur[N];
void init()
{
memset(head, -1, sizeof head);
cnt = 0;
}
void addedge(int u, int v, int w)
{
e[cnt] = {v, head[u], w, 0};
head[u] = cnt++;
e[cnt] = {u, head[v], 0, 0};
head[v] = cnt++;
}
bool bfs()//建分层图
{
queue<int> q;
memset(dep, 0, sizeof(int) * (n + 1));
dep[S] = 1;
q.push(S);
while (q.size())
{
int u = q.front();
q.pop();
for (int i = head[u]; ~i; i = e[i].nxt)
{
int v = e[i].v;
if ((!dep[v]) && (e[i].cap > e[i].flow))
{
dep[v] = dep[u] + 1;
q.push(v);
}
}
}
return dep[T];
}
int dfs(int u, int flow)
{
if ((u == T) || (!flow)) return flow;
int ret = 0;
for (int& i = cur[u]; ~i; i = e[i].nxt)//当前弧优化
{
int v = e[i].v, d;
if ((dep[v] == dep[u] + 1) &&(d = dfs(v, min(flow - ret, e[i].cap - e[i].flow))))
{
ret += d;
e[i].flow += d;
e[i ^ 1].flow -= d;
if (ret == flow) return ret;
}
}
if(ret!=flow) dep[u]=-1;//-1优化
return ret;
}
void dinic()
{
while (bfs())
{
memcpy(cur, head, sizeof(int) * (n + 1));
maxflow += dfs(S, INF);
}
}
} mf;
例题
养猪
尼克在一家养猪场工作,这家养猪场共有M间锁起来的猪舍,由于猪舍的钥匙都给了客户,所以尼克没有办法打开这些猪舍,客户们从早上开始一个接一个来购买生猪,他们到达后首先用手中的钥匙打开他所能打开的全部猪舍,然后从中选取他要买的生猪,尼克可以在此期间将打开的猪舍中的猪调整到其它开着的猪舍中,每个猪舍能存放的猪的数量是没有任何限制的。买完猪后客户会将他打开的猪舍关上。
好在尼克事先知道每位客户手中有哪些钥匙,要买多少猪,以及客户到来的先后次序。请你写一个程序,帮助尼克求出最多能卖出多少头生猪。
这题的主要问题是每次被打开的房间内的猪可以相互移动。为了解决这个问题,不妨换个角度来思考:实际上如果某客户取的猪是以前从其他的房间过来的,那么是不是可以就让这个客户到它原先所在的房间去取呢?即猪本身并不移动,而是钥匙重新分配,即客户拥有之前来的客户的某些钥匙。
例如客户1有3和4的钥匙,客户2有4和5的钥匙,那么客户2就等价拥有3、4和5这3把钥匙。又如果客户3有5和6的钥匙,他又等价拥有3、4、5和6的钥匙。
也就是说:只要某客户拥有的钥匙和之前的某些客户(他们的钥匙也有可能是别人给的)有交集,那么那些客户就相当于把他们的钥匙都给了这个客户。
这样按照顺序预处理后,客户前后到来的有序限制和猪可以移动的不利因素就不存在了,构图后求最大流即可。构图方式是:图中的点有客户和房间,增加源点和汇点,源点到房间连边,容量为房内猪的数量;客户到汇点连边,容量为客户的需求;房间到客户,只要客户有该房间的钥匙就连边,容量为无穷大。
网络流模型
当然 很多问题都能用网络流解决
关键在于如何建图
通常通过最小割转化为最大流
二选一模型
建模方式:
源点向每个物品连边,边权为收益,割掉该边表示不选该物品;
每个物品向汇点连边,边权为代价,割掉该边表示选该物品;
物品之间连边,边权和意义视约束而定。
最终答案=总收益-最小割。
最大权闭合子图模型
给定一张有向图,求一个权值和最大的点集S,使得S中任意点可达的点都在S内。
建模方式:
源点向点权为正的点连边,边权为点权,割掉该边表示不选该点;
点权为负的点向汇点连边,边权为点权的绝对值,割掉该边表示选该点;
将原图中的边照搬到新图上,边权为inf。
最终答案=正点权和-最小割。
费用流
在最大流中 我们贪心地在残量网络上寻找增广路增广
现在多了费用的情况下
我们应该在残量网络上沿着费用最小的路径增广
此时残量网络上反向边的费用应该是原边费用的相反数
也就是说会出现负边权
所以我们应该使用SPFA寻找最短路
所以算法的核心是最短路与最大流操作交替进行
在求最短路的时候顺便把图分层 可以进行多路增广
同样的 可以用当前弧优化 和 -1优化
#include <bits/stdc++.h>
using namespace std;
const int N = 5e3 + 5, M = 1e5 + 5;
const int INF = 0x3f3f3f3f;
int n, m, tot = 1, head[N], cur[N], ter[M], nxt[M], cap[M], cost[M], dis[N], ret;
bool vis[N];
void add(int u, int v, int w, int c)
{
ter[++tot] = v;
nxt[tot] = head[u];
head[u] = tot;
cap[tot] = w;
cost[tot] = c;
}
void addedge(int u, int v, int w, int c)
{
add(u, v, w, c);
add(v, u, 0, -c);
}
bool spfa(int s, int t)
{
memset(dis, 0x3f, sizeof(dis));
memcpy(cur, head, sizeof(head));
std::queue<int> q;
q.push(s), dis[s] = 0, vis[s] = 1;
while (!q.empty())
{
int u = q.front();
q.pop(), vis[u] = 0;
for (int i = head[u]; i; i = nxt[i])
{
int v = ter[i];
if (cap[i] && dis[v] > dis[u] + cost[i])
{
dis[v] = dis[u] + cost[i];
if (!vis[v]) q.push(v), vis[v] = 1;
}
}
}
return dis[t] != INF;
}
int dfs(int u, int t, int flow)
{
if (u == t) return flow;
vis[u] = 1;
int ans = 0;
for (int &i = cur[u]; i && ans < flow; i = nxt[i])
{
int v = ter[i];
if (!vis[v] && cap[i] && dis[v] == dis[u] + cost[i])
{
int x = dfs(v, t, std::min(cap[i], flow - ans));
if (x) ret += x * cost[i], cap[i] -= x, cap[i ^ 1] += x, ans += x;
}
}
vis[u] = 0;
return ans;
}
int mcmf(int s, int t)
{
int ans = 0;
while (spfa(s, t))
{
int x;
while ((x = dfs(s, t, INF))) ans += x;
}
return ans;
}
int main()
{
int s, t;
scanf("%d%d%d%d", &n, &m, &s, &t);
while (m--)
{
int u, v, w, c;
scanf("%d%d%d%d", &u, &v, &w, &c);
addedge(u, v, w, c);
}
int ans = mcmf(s, t);
printf("%d %d\n", ans, ret);
return 0;
}
例题
这回真写完了 撒花撒花
引用来源
