Splay

前言

学到Splay 感觉网上的资料多了好多

果然是常用的 那得好好学

Splay树是一种平衡二叉查找树

它通过旋转操作保持树的平衡而不至于退化成链

能够在均摊复杂度$O(log N)$时间内完成插入，查找和删除操作

提一句

Splay是Tarjan发明的

Tarjan好强

---

算法介绍

二叉查找树

既然Splay是一种平衡的二叉查找树，我们得先知道普通的二叉查找树

二叉查找树(BST) 是具有下列性质的二叉树

若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值；

若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值；

它的左、右子树也分别为二叉查找树

它的中序遍历是有序的

附个图

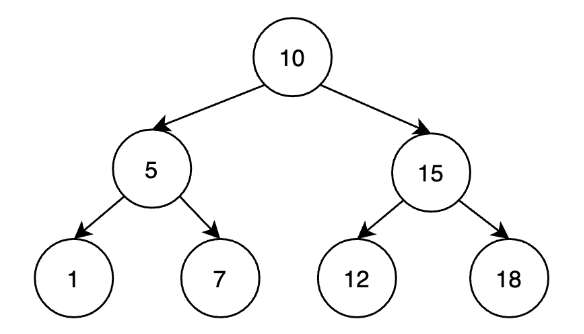
它能在最优$O(log$ $n)$的时间复杂度内完成查询，修改等操作

但是 如果出题人不讲武德

那就劝他好自为之

从小到大给数据 BST就退化成了一条链

时间复杂度达到了$O(n)$

于是我们要用Splay的旋转操作避免退化

---

Splay

splay维护以下信息

在每次操作时，Splay会通过一次次旋转，将树的结构改变(也就是伸展操作splay)，把当前结点转到树根上

这个操作使得Splay的均摊时间复杂度为$O(log$ $n)$

所以到底怎么旋转呢

---

操作

旋转Rotate(x)

旋转操作：

将指定的结点x向上移动一级

将原有的父节点作为自己的儿子

并且维持BST的性质

旋转分为左旋和右旋 但是我们把他们结合在一起

详情看代码 配合图片食用更佳

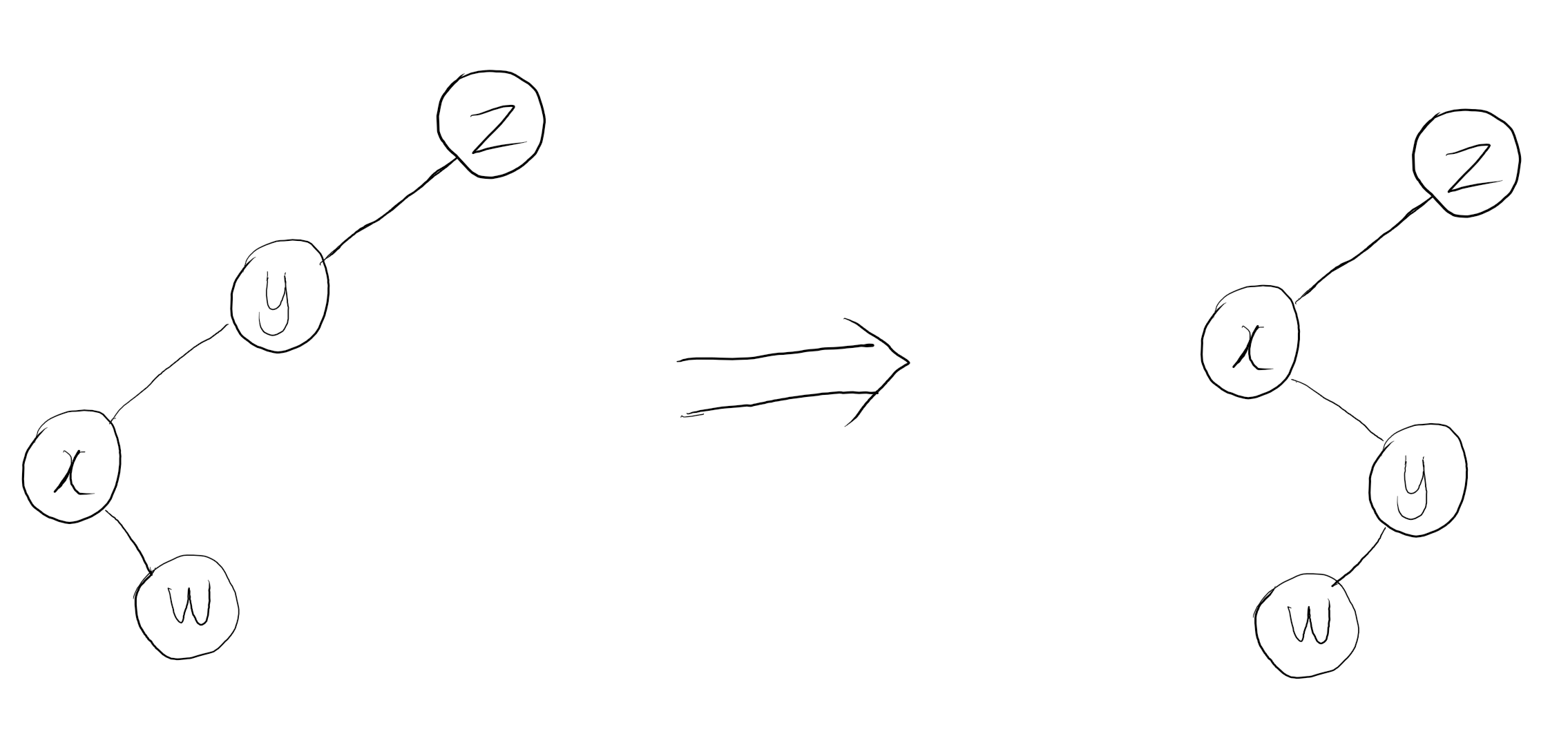
#define lc(x) tree[x].ch[0]
#define rc(x) tree[x].ch[1]
#define fa(x) tree[x].fa
int root,cnt;
bool Check(int x)
//查询x是在左子树还是右子树
//右子树返回1 左子树返回0
{
    return rc(fa(x))==x;
}
void Pushup(int now)
{
    tree[now].siz=tree[lc(now)].siz+tree[rc(now)].siz+tree[now].cnt;
}
void Rotate(int x)
{
    //y为x的父节点
    //z为y的父节点
    //选取不与x同侧的x的子节点w 以维持BST性质
    int y=fa(x);
    int z=fa(y);
    int k=Check(x),w=tree[x].ch[k^1];
    tree[z].ch[Check(y)]=x,fa(x)=z;//把x接在z下
    tree[y].ch[k]=w,fa(w)=y;//把w接在y下
    tree[x].ch[k^1]=y,fa(y)=x;//把y接在x下
    Pushup(y),Pushup(x);
}

---

伸展Splay(x,target)

这个操作将x调整为target的子节点

它分四种情况 需要分别处理

1. target是x的父节点 结束
2. target是x的父亲的父亲 rotate(x)

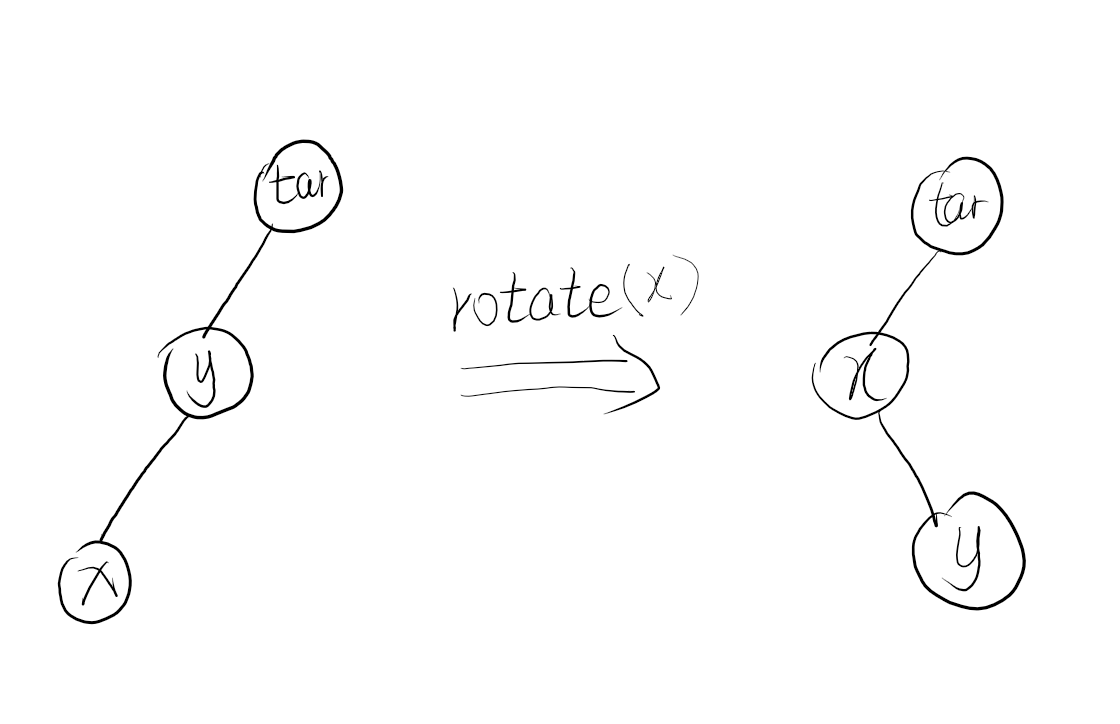
3. 直线型(x的父亲的父亲不是target) rotate(y),rotate(x) 先父后儿

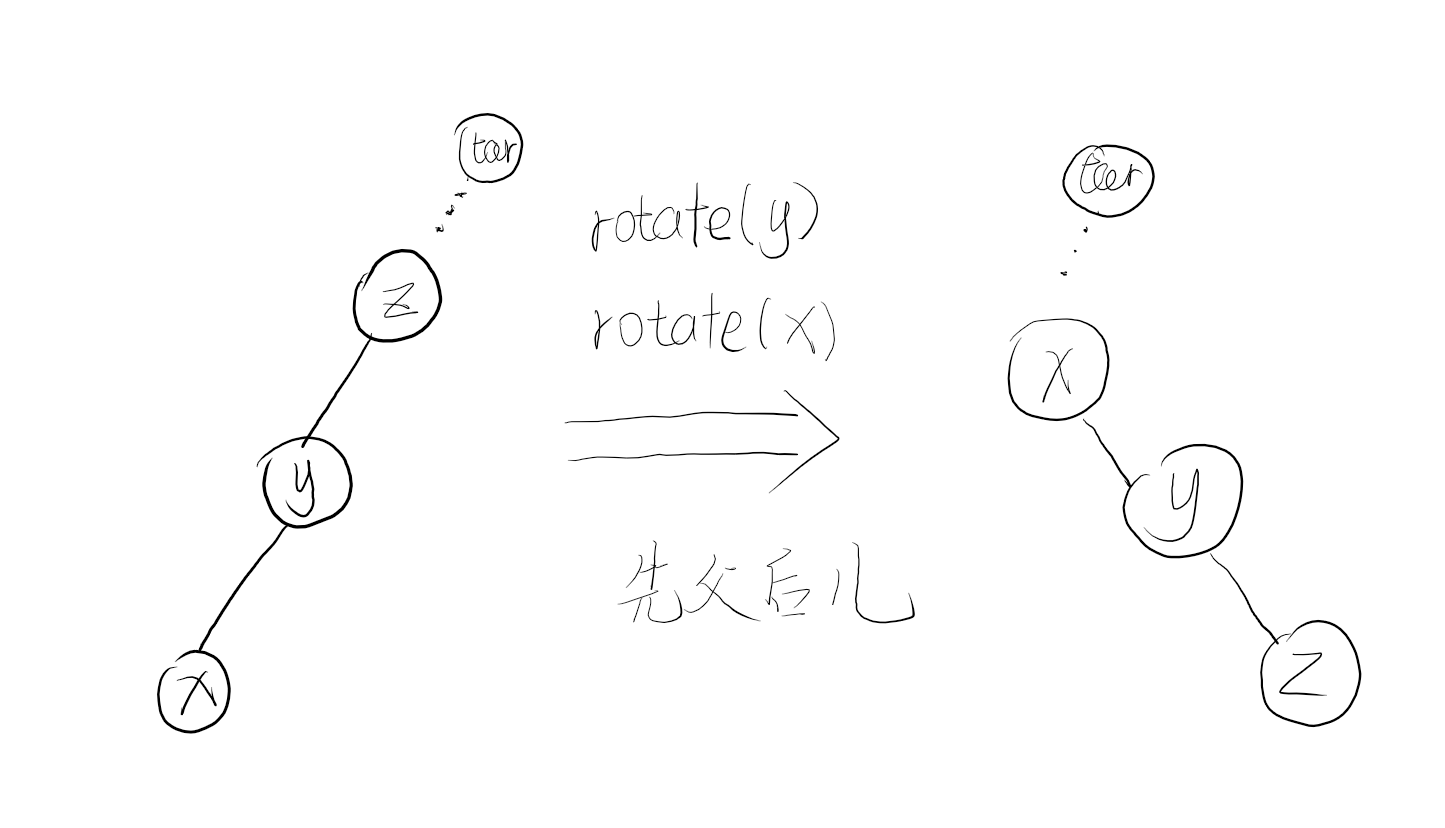
4. 折线型(x的父亲的父亲不是target) rotate(x),rotate(x) 先儿后儿

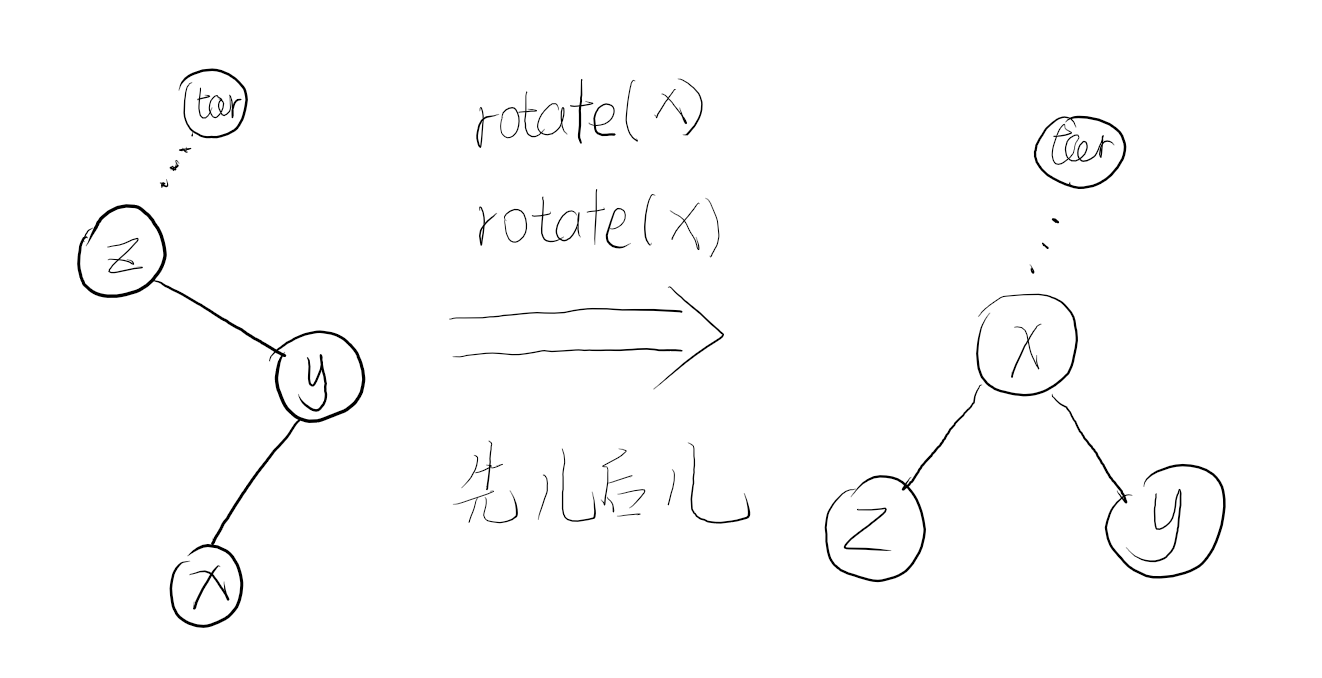
如果我们想将x转到根节点

只需要让target等于0即可

Splay的代码如下

void Splay(int x,int target=0)
//如果调用的时候写Splay(x) 默认target=0
//如果调用的时候写Splay(x,target) target为传入的值
{
    while(fa(x)!=tarjat)
    {
        int y=fa(x),z=fa(y);
        if(z!=target)
        {
            if(Check(x)==Check(y)) //直线型
                Rotate(y);
            else//折线形
                Rotate(x);
        }
        Rotate(x);
    }
    if(!target)
        root=x;
}

---

查询Find(v)

判断元素v是否在伸展树表示的有序集中 并把它转到根

设当前结点为x

若v大于x 向右子树找

若v小于x 向左子树找

若v等于x 找到了 把x转到根

若访问到空节点 表示没找到

void Find(int val)
{
    int now=root;
    while(tree[now].ch[val>tree[now].val] && tree[now].val!=val)
        now=tree[now].ch[val>tree[now].val];
    Splay(now);
}

---

插入Insert(v)

跟查询差不多

设当前结点为x

若v大于x 向右子树找

若v小于x 向左子树找

若v等于x 找到了 cnt++

若访问到空节点 新建一个点

void Insert(int val)
{
    int now=root,las=0;
    while(now && tree[now].val!=val)
    {
        las=now;
        now=tree[now].ch[val>tree[now].val];
    }
    if(now)//找到了 个数加1
        ++tree[now].cnt;
    else//没找到 新建点
    {
        now=++cnt;
        if(las)
            tree[las].ch[val>tree[las].val]=now;
        lc(now)=rc(now)=0;
        tree[now].val=val;
        fa(now)=las;
        tree[now].siz=tree[now].cnt=1;
    }
    Splay(now);
}

---

其他操作

合并Join(u,v)

u,v分别是需要合并的子树S1,S2的根节点

需要满足S1的所有元素都小于S2的所有元素

首先找到S1的最大点x 转到根

然后把S2当作x的右子树即可

删除Del(x)

先找到x 转到根

然后把左右子树合并

查询排名Getrank(v)

先找到v所在的结点x 转到根

排名为左子树结点个数+1

分裂Split(v)

先找到v所在的结点x 转到根

取出左右子树即可

---

到此Splay就写差不多了

附例题

P3369 【模板】普通平衡树

P3391 【模板】文艺平衡树

---

引用来源

Splay入门_splay zigzag-CSDN博客

Splay 树 - OI Wiki (oi-wiki.org)

二叉搜索树_百度百科 (baidu.com)

还有书