无旋式Treap

前言

无旋Treap,又称fhq_treap,是范浩强大佬发明的一种数据结构

它也是一棵平衡二叉搜索树

普通的Treap通过旋转来保持平衡

而fhq treap不需要旋转就可以维持平衡

它可以支持一切Treap和Splay等平衡树的操作,支持可持久化

对于初学者来说,它比Splay好学,比Treap好用,实在不失为一个性价比极高的数据结构.

大家对它评价好高啊

要好(四声) 好(三声) 学

(梅姐又出现了)

---

Treap

Treap就是由Tree和Heap(树和堆)两种数据结构组合而成的数据结构。

Treap与BST不同的是

它的每个结点除了权值(val,key)以外，还维护了一个随机优先级pri[x]

在Treap中 权值 维护题目要求的信息 满足BST性质

在Treap中 优先级满足小根堆的性质(梦回左偏树)

例如

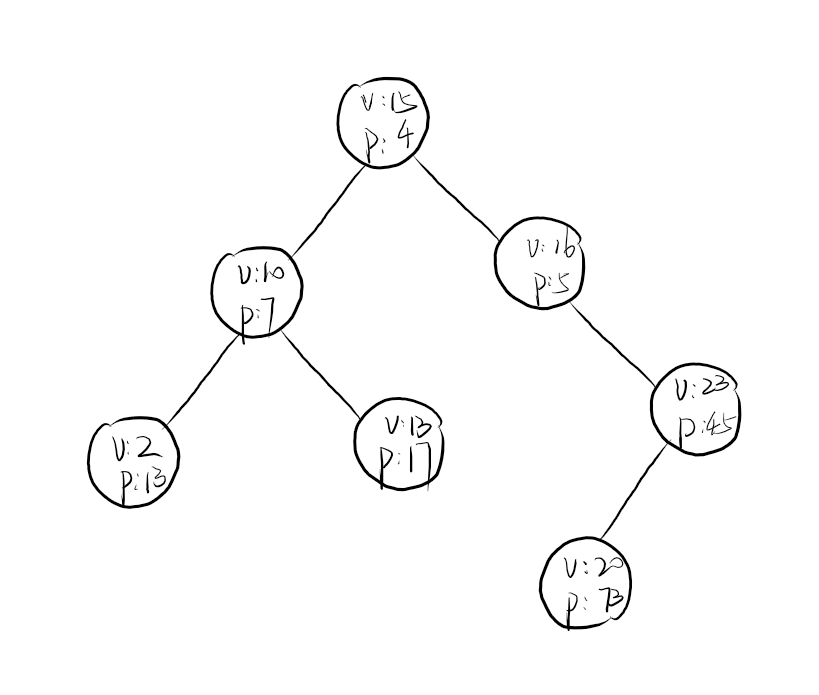
因为优先级是随机生成的，所以它是期望平衡的

有旋式Treap和无旋式Treap建出的树都是上面那样的

只不过维护平衡的方式不同

有旋式Treap是如何旋转的这里不讲(因为我没学，好像没人用)

下面来学无旋式Treap的操作

无旋式Treap

总的来说 它是靠合并和开裂维持平衡的

合并

将两棵有序(x中元素的权值都小于y中元素的权值)的treap合并成一棵

详见代码

int Merge(int x,int y)
{
    if(!x|| !y) return x+y; //一棵树为空 返回另一棵树
    if(tree[x].pri<tree[y].pri)//若x的优先级小 x作根
    {
        tree[x].r=Merge(tree[x].r,y);//由于x中权值比y小，所以合并右子树与y
        pushup(x);
        return x;
    }
    else//若y的优先级小 y作根
    {
        tree[y].l=Merge(x,tree[y].l);//由于x中权值比y小，所以合并左子树与x
        push_up(y);
        return y;
    }
}

---

分裂

1. 按权值分裂 Split(now,val,x,y)

将一个Treap分裂为两个，第一个Treap所有节点的权值小于等于给定$val$值，第二个Treap所有节点的权值大于等于给定$val$值。

详见代码

void Split(int now,int val,int &x,int &y)
{
    if(!now)
        x=y=0;
    else
    {
        if(tree[now].val<=val)//now的权值小于val，说明左子树都小 不用分了 去分右子树
        {
            x=now;
            Split(tree[now].r,val,tree[now].r,y);
        }
        else//now的权值大于val 说明右子树都大 不用分了 去分左子树
        {
            y=now;
            Split(tree[now].l,val,x,tree[now].l);
        }
        pushup(now);
    }
    return ;
}

2. 按大小分裂 Split(now,size,x,y)

将一个Treap分裂为两个，x的大小为$size$，储存着$now$树中前$size$小的元素

详见代码

void Split(int now,int size,int &x,int &y)
{
    if(!now)
        x=y=0;
    else
    {
        pushdown(now);
        if(tree[tree[now].l].size<size)//左子树大小不够size 去分右子树
        {
            x=now;
            Split(tree[now].r,size-tree[tree[now].l].size-1,tree[now].r,y);
        }
        else//否则分左子树
        {
            y=now;
            Split(tree[now].l,size,x,tree[now].l);
        }
        update(now);
    }
    return ;
}

---

插入

Insert(val) 在treap中插入一个值为val的元素

新建一个节点,然后根据权值拆成左右子树,然后Merge(Merge(左,新节点),右)即可

---

建树

当我发出fhq treap如何建树这个问题的时候

@ 聪明的xixi告诉我一个个插入

这确实是一种方法

还有可以利用笛卡尔树的$O(n)$建树的方法

算法杂记 | 笛卡尔树 - 知乎 (zhihu.com)

这里有

---

删除

根据权值拆成左右子树和要拆除的节点,然后直接Merge(左,右)即可

区间操作

一般来讲是通过Split剖出需要操作的区间代表的子树,然后在根节点打标记,然后合并即可.

合并无序的两棵树

int AllMerge(int x,int y)
{
    if(!x || !y) return x+y;
    if(tree[x].pri>tree[y].pri)
        swap(x,y);
    int a,b;
    split(y,tree[x].val,a,b);
    lc(x)=AllMerge(lc(x),a);
    rc(x)=AllMerge(rc(x),b);
    pushup(x);
}

fhq treap的基本操作就到此为止了

合并和开裂是关键

撒花

---

附例题

【模板】普通平衡树 - DL24JPOJ

P3391 【模板】文艺平衡树

---

引用来源

数据结构-Treap(树堆) 详解-CSDN博客

算法｜学习笔记：史上最简单的平衡树——无旋Treap - 知乎 (zhihu.com)