Copyright By

注意事项

讲评人没有实力，也没有烤鸭皮皮，所以对于接下来提到的一些结论将不予证明，感兴趣的可以自己bdfs一下，或者课后询问讲评人

部分定义不准确，并不形式化，是讲评人自己思考后的结果

如果觉得自己的想法与讲评人有不同或者算法更优，可提出自己的见解

---

（这边因为网寄了就不找图了）

引入

如何在一个有向无环图上表示一个字符串的所有子串

把每一个后缀加入trie树即可

但是这样节点是$O(n^2)$的

所以想办法构造一个节点数、边数尽量小并满足相应性质的有向无环图——后缀自动机

性质

懒得打字了看书吧~

构造

首先sam的节点数最多$2n$，数组注意开2倍

空间复杂度$O(mn)$,m为有多少种字符，通常26或52

所以sam还是只能处理1e6的数据

时间复杂度全部$O(n)$

首先贴出代码：

static constexpr int AwA = 1e6 + 10;

struct SAMNode {
    int ch[26];
    int len, fa, cnt;
} tr[AwA << 1]{};

int np = 1, tot = 1;
char s[AwA]{};
int n{};

inline void AddSAM(int ch) {
    int p = np;
    np = ++tot;
    tr[np].len = tr[p].len + 1;
    tr[np].cnt = 1;
    while (p && !tr[p].ch[ch]) {
        tr[p].ch[ch] = np;
        p = tr[p].fa;
    }

    //case 1
    if (!p) {
        tr[np].fa = 1;
        return;
    }

    int q = tr[p].ch[ch];
    //case 2
    if (tr[p].len + 1 == tr[q].len) {
        tr[np].fa = q;
        return;
    }

    //case 3 split
    int nq = ++tot;
    memcpy(tr[nq].ch, tr[q].ch, sizeof tr[nq].ch);
    tr[nq].len = tr[p].len + 1;
    tr[nq].fa = tr[q].fa;

    tr[q].fa = tr[np].fa = nq;
    while (p && tr[p].ch[ch] == q) {
        tr[p].ch[ch] = nq;
        p = tr[p].fa;
    }
}

可以看出sam是在线算法

算了还得找图

（此处图来自董晓算法）

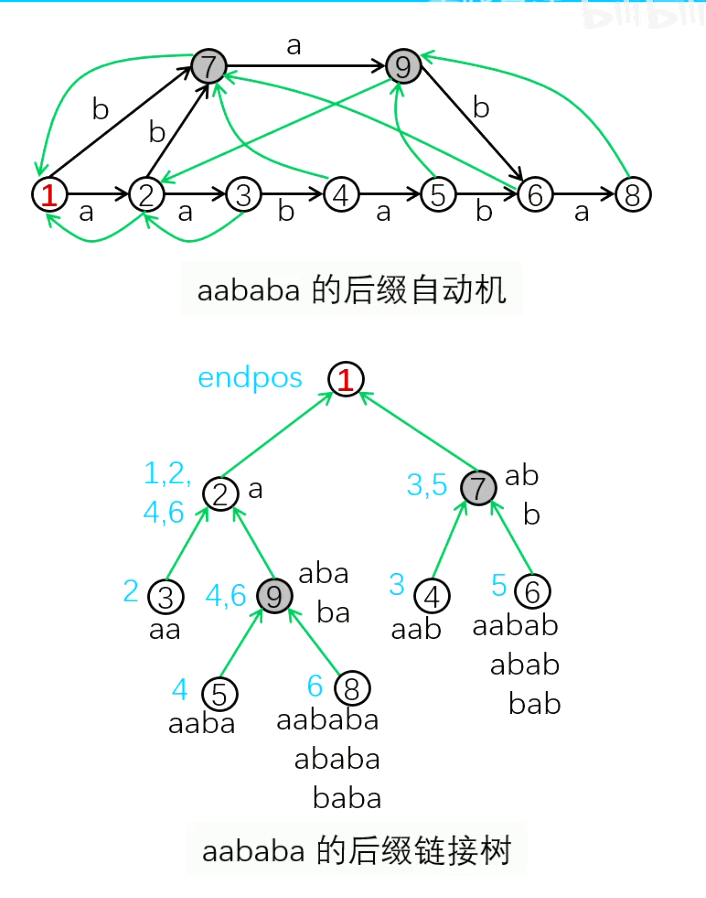
图中黑色边为转移边，从根节点沿着转移边走会走出原串的子串，且每个子串只能被走出一次，到达位置就是该子串的endpos类

绿边为链接边，表示了endpos的父子关系

分析代码：

在插入新的字符前，前面的字符已经构成了一个sam

np记录了这个sam的终止节点

接下来在存储后缀的链上跳，如果没有相应的子节点就直接连边

若跳到根节点直接返回

接下来敲不动了请听讲评人bb

经过一阵噼里啪啦的讲题

好的那么我们就构造完了

---

对于每个点endpos中有几个数，及该点子串总共有几个

我们记cnt

如果是正常节点初始cnt为1

如果是添加的节点cnt就只能从子节点转移，所以初始为0

接着把cnt加上子节点的cnt

就完事了

可在链接树上dfs或者拓扑排序（可用计数排序实现）

完结撒花