- zyssssss 的博客
递归
- @ 2024-1-18 9:22:58
递归
最最首先
欢迎大家来到大连二十四中学金普学校
提前声明:
可能需要一些C++基础才能看懂所有的东西
如果你没有基础
那就睡觉吧
开个玩笑
其实不要紧
只需要理解思想
不需要完全理解代码
如果你感到听不懂
深呼吸 听不懂是正常的
有部分结论 代码 题目 来自网络
在文后有链接 侵删
前言
什么是递归?
函数反复调用自身即是递归
举个栗子
我在这篇博客里写了这篇博客的链接
像不像套娃
举个正经栗子
比如我们算的阶乘
(阶乘就是)
以为例
=> *
=> * *
=> * * *
=> * * * *
=> * * * * *
=> * * * * *
=> * * * *
=> * * *
=> * *
=> *
=>
看到递归了吗?
代码写出来是这样的
#include<bits/stdc++.h>
using namespace std;
int get(int n)
{
if(n==1)//回归
return 1;
else//递进
return n*get(n-1);//函数自己调用了自己
}
int main()
{
cout<<get(6)<<endl;
return 0;
}
先递进,再回归——这就是「递归」
通俗来讲 递归是一种懒人的甩锅思想
如果你自己计算不了
就甩给你的下级去做
我们不能成为这样的人
甩锅的过程就是函数调用自身
递归也可以看作是一个编程技巧
也是一种将规模大的问题转化为规模小的问题的思想
组成部分
明白了什么是递归之后
我们就要知道递归是怎么实现的
递归由两部分组成
- 递归的终止条件
递归不能无终止的进行下去
一个老板把工作交给了经理
经理又交给了员工
员工总不能把工作给保洁阿姨吧
比如上面的例子
我们算到f(1)的时候就停止了
因为地球人都知道1的阶乘是1
我们总不能再去算0和-1的阶乘吧
如果我们再去不停的调用
程序就会死循环
所以递归的终止条件是十分重要的
if(n==1)
return 1;
上面代码的这一句就是例题的终止条件
如果你写代码时不注意这一点
就会像下图一样看见满屏的错误
- 递归关系
这个就跟具体问题有关系了
还是之前的例子
我们要算6的阶乘 首先要知道5的阶乘
要算5的阶乘 首先要知道4的阶乘
要算i的阶乘 首先要知道i-1的阶乘
所以我们计算f(i)时 调用的是f(i-1)
再看一眼代码
#include<bits/stdc++.h>
using namespace std;
int get(int n)
{
if(n==1)
return 1;
else
return n*get(n-1);//函数自己调用了自己
}
int main()
{
cout<<get(6)<<endl;
return 0;
}
例题
1.兔子数列
兔子数列又称斐波那契数列
1,1,2,3,5,8,13...这样一个数列就是斐波那契数列,我们要求第n项的值。
观察数列可得
除了第一项和第二项,所有的数列的值都是前一项和前一项的前一项的和
转换成函数也就是f(n) = f(n-1) + f(n-2)
我们从递归的终止条件和递归关系去入手
首先分析递归的终止条件
斐波那契数列的第1项和第2项是特殊的 都是1
所以我们算到第1项或第2项就可以返回了
也就是
if(n==1 || n==2)
return 1;
然后再分析递归关系
斐波那契的第n项是第n-1项和第n-2项的和
我们要算第n项
就要知道第n-1项 和第n-2项
所以是这么调用的
else
return f(n-1)+f(n-2);
总的代码是这样的
const int mod = 1000000007;
struct Matrix {
int a[3][3];
Matrix() { memset(a, 0, sizeof a); } // 构造函数,矩阵初始化全零
Matrix operator*(const Matrix &b) const {
Matrix res;
for (int i = 1; i <= 2; ++i)
for (int j = 1; j <= 2; ++j)
for (int k = 1; k <= 2; ++k)
res.a[i][j] = (res.a[i][j] + a[i][k] * b.a[k][j]) % mod;
return res;
}
} ans, base;
void init() { // 初始化 ans、base 矩阵
base.a[1][1] = base.a[1][2] = base.a[2][1] = 1;
ans.a[1][1] = ans.a[1][2] = 1;
}
void qpow(int b) { // 求
while (b) {
if (b & 1) ans = ans * base;
base = base * base;
b >>= 1;
}
}
int main() {
int n = read();
if (n <= 2) return puts("1"), 0;
init();
qpow(n - 2);
println(ans.a[1][1] % mod);
}
好像是矩阵快速幂 对不起 重来
只是想给大家整个乐子
下面是正经的
#include<bits/stdc++.h>
using namespace std;
int f(int n)
{
if(n==1 || n==2)
{
return 1;
}
else
{
return f(n-1)+f(n-2);
}
}
int main()
{
int n;
cin>>n;
cout<<f(n)<<endl;
return 0;
}
练习
代码跟上面一样
这道题多组数据
AC代码
#include<bits/stdc++.h>
using namespace std;
int f(int n)
{
if(n==1 || n==2)
{
return 1;
}
else
{
return f(n-1)+f(n-2);
}
}
int main()
{
int n;
cin>>n;
while(n--)
{
int a;
cin>>a;
cout<<f(a)<<endl;
}
return 0;
}
递归关系稍有变化
注意取模
不放代码了 自己回家慢慢做
加油
2.累加和
求的结果
递归的终止条件是算到1的时候返回1
递归关系是
代码如下
#include<bits/stdc++.h>
using namespace std;
int f(int n)
{
if(n==1)
{
return 1;
}
else
{
return n+f(n-1);
}
}
int main()
{
int n;
cin>>n;
cout<<f(n)<<endl;
return 0;
}
题目链接在这里
3.累乘积
求的结果
这题是最开始的例子推广到了n
其实是一样的
也是把上一题的加改为乘
递归的终止条件是算到1的时候返回1
递归关系是
#include<bits/stdc++.h>
using namespace std;
int f(int n)
{
if(n==1)
{
return 1;
}
else
{
return n*f(n-1);
}
}
int main()
{
int n;
cin>>n;
cout<<f(n)<<endl;
return 0;
}
刚才大佬yzy已经讲完了很多种排序算法
不能只学会了冒泡吧
接下来再说两个算法
快速排序和归并排序
试图理解思想
不需理解代码
快速排序
快速排序是一个基于分治的排序方法
没学分治不要紧 明天有大佬wcj讲
给定一个数组a,该数组共有n个元素,我们需要对其进行从小到大的排序。
假设要排序的区间为
如果区间长度小于等于 1,那就直接退出(因为只有一个元素不用排序)
这就是递归的终止条件
否则在该区间中选择任意一个元素x作为基准元素。将大于x的元素放到x的右边;将小于x的元素放到x的左边
再对x的左右两边的区间分别进行递归即可。
这就是递归关系
我们看图模拟一下这个过程
图片来源
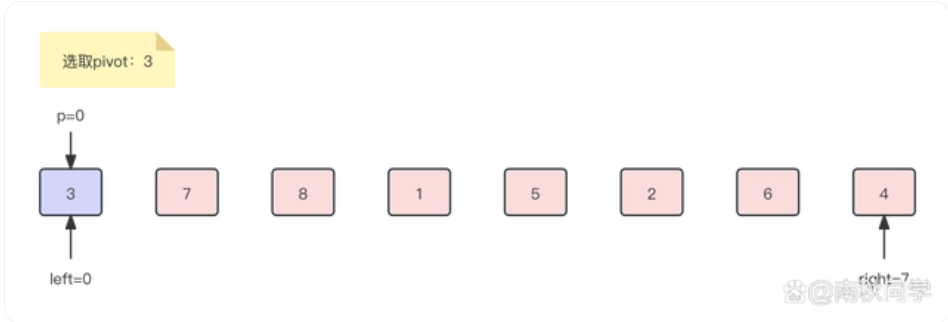
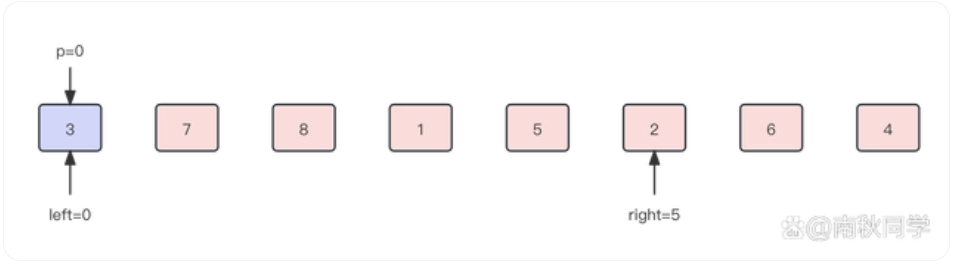
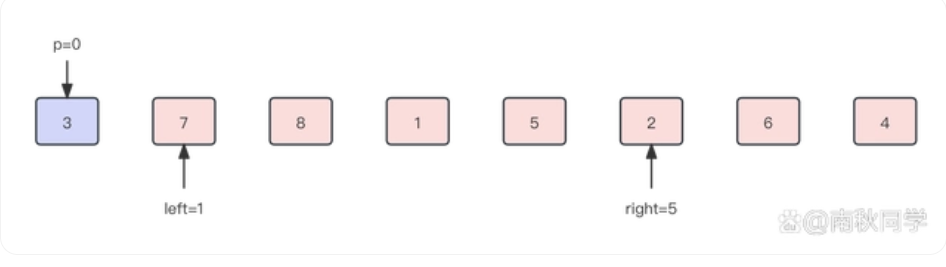
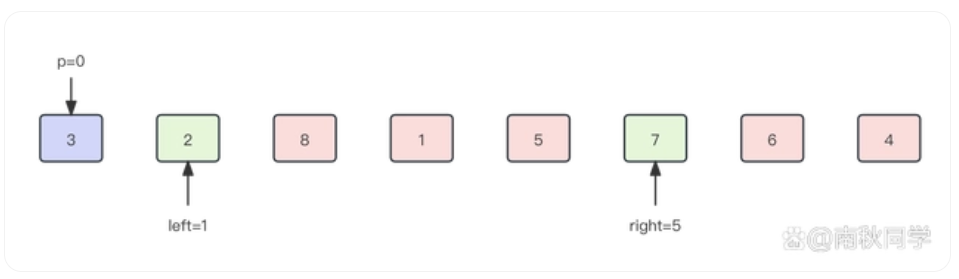
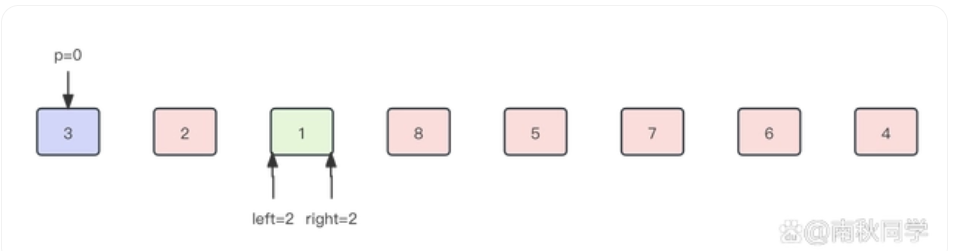
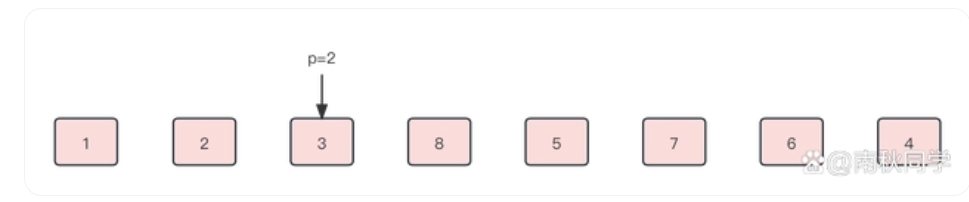
代码如下
能看到函数调用自身的递归操作
void quick_sort(int l,int r){
//区间 [l,r] 的元素个数为 r - l + 1
//如果区间元素个数 <= 1 就直接返回,即 r - l + 1 <= 1
//化简一下就是 l >= r
if(l >= r) return;
swap(a[l] , a[l + rand() % (r - l + 1)]);//随机选择元素
int x = a[l];
int i = l ,j = r;
while(i < j){
//先从右往左找到第一个 <= x 的元素
while(i < j && a[j] > x) j--;
//把找到的元素放到位置 i 上
if(i < j) a[i++] = a[j];
//再从左往右找到第一个 >= x 的元素
while(i < j && a[i] < x) i++;
//把找到的元素放到位置 j 上
if(i < j) a[j--] = a[i];
}
//最后,i 和 j 同时指向了同一个位置 p
//我们就把 a[p] 的值赋为 x
//x 的位置就已经确定了
a[i] = x;
//再递归的处理剩下的两个区间,即 [l , p - 1] 和 [p + 1 , r]
quick_sort(l,i-1);
quick_sort(i+1,r);
}
归并排序
归并排序,是创建在归并操作上的一种有效的排序算法。
归就是层层递归将数列分开
并就是把排序好的左右数列合并
合并时每次选择左右序列比较小的那个元素
看图理解一下
图片来源
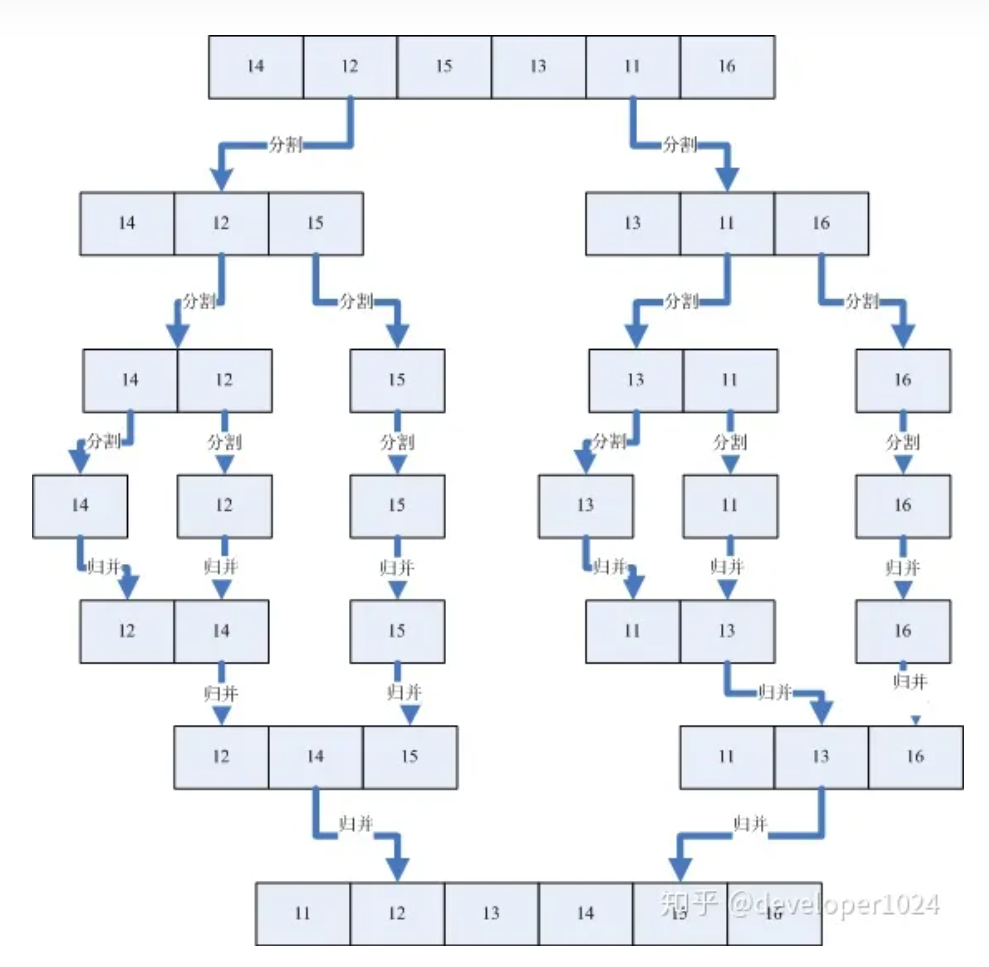
上图中首先把一个未排序的序列从中间分割成2部分,再把2部分分成4部分,依次分割下去,直到分割成一个一个的数据(递归的终止条件),再把这些数据两两归并到一起,使之有序,不停的归并,最后成为一个排好序的序列
代码如下
同样能看到函数调用自身的递归操作
void _MergeSort(int* arr, int begin, int end, int* tmp)
{
if (begin >= end)
{
return;
}
//分治递归,让子区间先有序
int mid = (begin + end) / 2;
_MergeSort(arr, begin, mid, tmp);
_MergeSort(arr, mid + 1, end, tmp);
int begin1 = begin;
int end1 = mid;
int begin2 = mid + 1;
int end2 = end;
int i = begin1;
//在arr[begin1,end1]和arr[begin2,end2]两个区间中开始归并
while ((begin1 <= end1) && (begin2 <= end2))
{
//如果arr[begin1]的值小,就让arr[begin1]的值先进入tmp数组
if (arr[begin1] < arr[begin2])
{
tmp[i++] = arr[begin1++];
}
//如果arr[begin2]的值小于等于arr[begin1],就让arr[begin2]的值进入tmp数组
else
{
tmp[i++] = arr[begin2++];
}
}
//如果数组1中的数据还没有归并到tmp中完,就直接将剩下的都放到tmp中
while (begin1 <= end1)
{
tmp[i++] = arr[begin1++];
}
//如果数组2中的数据还没有归并到tmp中完,就直接将剩下的都放到tmp中
while (begin2 <= end2)
{
tmp[i++] = arr[begin2++];
}
//把归并数据拷贝到原数据
memcpy(arr + begin, tmp + begin, sizeof(int) * (end - begin + 1));
}
void MergeSort(int* arr, int n)
{
//归并排序需要先申请一个辅助数组
int* tmp = (int*)malloc(sizeof(int) * n);
if (tmp == NULL)
{
perror("MergeSort malloc fail");
exit(-1);
}
_MergeSort(arr, 0, n - 1, tmp);
}
到此递归就讲完了
其实是讲不完的
因为递归很常用
学是学不完的
之后的无数算法要用到递归思想
所以要打好基础
回家好好看看
加油加油
引用来源
「一发入魂」一文彻底搞懂快速排序算法 (baidu.com)
【算法】排序算法之归并排序 - 知乎 (zhihu.com)
只供学习使用 侵删
