网格图覆盖问题
该比赛已结束,您无法在比赛模式下递交该题目。您可以点击“在题库中打开”以普通模式查看和递交本题。
题目背景
莫得。
题目描述
- 有一个 行 列网格图,现有 种颜色,每个格子都被染成 种颜色之一(不保证每种颜色都出现了)。
- 对于每一种颜色,请你求出能覆盖所有该颜色格子的最小的正方形的面积。
- 正方形不可旋转,正方形可以超出网格图边界。
输入格式
从 cover.in 读入。
- 第一行,三个正整数 ,
- 接下来 行,每行 个数 ,表示第 行第 列的格子,颜色为 。
输出格式
输出到 cover.out。
- 一行 个整数,每行一个非负整数,表示最小的正方形覆盖面积。
输入输出样例
3 5 2
1 2 1 2 2
1 1 2 2 2
2 2 2 2 2
9
25
样例解释
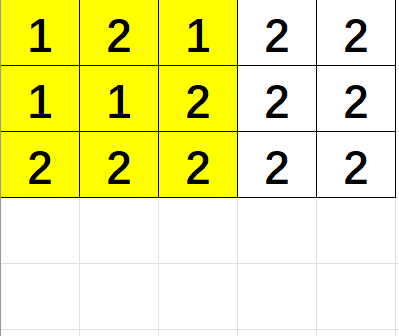
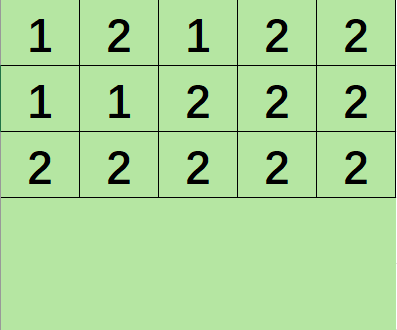
- 颜色 ,颜色 的一种可能的最优覆盖方式如上。
数据范围
子任务
| 子任务编号 | 分值 | 限制 |
|---|---|---|
| 1 | 50 | |
| 2 | N/A |
- 大样例下载
- 编号为 的大样例满足编号为 的子任务的限制
